Дифференциальные уравнения для "чайников". Примеры решения

Контрольные вопросы:

1. Какая функция называется сеточной?

2. Какое уравнение называется разностным?

3. Какие уравнения называются разностными уравнениями 1-го порядка?

4. Как находится общее решение неоднородного разностного уравнения 1-го порядка?

5. Какое решение разностного уравнения называется фундаментальным?

6. Почему общее решение однородного уравнения с постоянными коэффициентами имеет вид геометрической прогрессии?

Задания.

1. Написать процедуру решения разностного уравнения первого порядка с начальным условием .

2. Для заданного уравнения найти общее и частное решение аналитически.

3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.

4. Выяснить, как влияет на результат возмущение начального условия, коэффициентов уравнения, правой части.

Найдем общее решение разностного уравнения 1-го порядка

. (1)

Частное решение однородного уравнения при получим, используя рекуррентную формулу: . Поскольку значение Y в каждом следующем узле сетки удваивается, получается геометрическая прогрессия со знаменателем q=2:

Частное решение неоднородного уравнения найдем в виде:, где А - неопределенный коэффициент. Тогда , , и, приравняв полученное значение к заданной правой части, найдем неопределенный коэффициент A=. Окончательно, общее решение: .

Используя начальное условие , находим константу: . Окончательно, частное решение при заданном начальном условии:

.

Для исследования устойчивости решения к возмущению самого решения и начального условия рассмотрим следующее уравнение:

с возмущенным начальным условием

(здесь - величина возмущения). Вычитая исходное уравнение (1), получим разностное уравнение для возмущения:

с начальным условием . Решение этого уравнения имеет вид: , т.е. даже малое возмущение в каком-либо узле экспоненциально растет с увеличением номера узла.

Студенту необходимо проиллюстрировать сказанное выше: исследовать влияние возмущений начального условия, правых частей и коэффициентов уравнения, изменив рекуррентную формулу.

Вариант, в соответствии с номером студента по списку в журнале, необходимо решить на языке программирования C++ (допускается использование среды Builder) или Pascal (допускается использование среды Delphi).

1. Рекуррентная формула для получения численного решения.
2. Аналитическое решение разностного уравнения. Общее решение и частное решение, удовлетворяющее заданным начальным условиям.
3. Исследовать устойчивость решения к возмущению начального условия и решения аналитически.

б) при возмущении коэффициентов уравнения;

в) при возмущении правой части.

Тема:Разностные уравнения 2 порядка

Контрольные вопросы:

1. Какие уравнения называются разностными уравнениями 2-го порядка?

2. Что такое характеристическое уравнение?

3. Как выглядит частное решение однородного разностного уравнения 2-го порядка с действительными корнями характеристического уравнения?

4. Как выглядит частное решение однородного разностного уравнения 2-го порядка с комплексными корнями характеристического уравнения?

5. Как находится общее решение неоднородного разностного уравнения 2-го порядка?

6. Что такое численное и аналитическое решение разностного уравнения 2-го порядка?

7. Какие задачи называются хорошо обусловленными?

Задания

1. Написать процедуру решения разностной краевой задачи для уравнения второго порядка с граничными условиями , .

2. Для заданного уравнения найти общее и частное решение аналитически и проверить критерий обусловленности.

3. Сравнить результаты вычислений по рекуррентной формуле с аналитическим решением.

4. Выяснить, как влияет на результат возмущение граничных условий и правой части.

РАЗНОСТНЫЕ УРАВНЕНИЯ - уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, ..., xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени.

Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность

y = y(t+1) – y(t),

которую часто называют первой разностью. При этом различают правую и левую разности, в частности

y = y(t) – y(t–1)

Левая, а приведенная выше - правая. Можно определить вторую разность:

Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) –

– 2y(t + 1) + y(t)

и разности высших порядков Δn.

Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке:

f = 0.

Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек

y(t), y(t+1), ..., y(t+n).

При этом разность между последним и первым моментами времени называется порядком уравнения.

При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю.

При исследовании функций многих переменных по аналогии с частными производными (см. Производная) вводятся также частные разности.

Линейные разностные уравнения первого порядка

y(x + 1) − ay(x) = 0. Линейное однородное разностное уравнение первого порядка с постоянными коэффициентами.

y(x + 1) − ay(x) = f(x). Линейное неоднородное разностное уравнение первого порядка с постоянными коэффициентами.

y(x + 1) − xy(x) = 0.

y(x + 1) − a(x − b)(x − c)y(x) = 0.

y(x + 1) − R(x)y(x) = 0, где R(x) -- рациональная функция.

y(x + 1) − f(x)y(x) = 0.

y(x + a) − by(x) = 0.

y(x + a) − by(x) = f(x).

y(x + a) − bxy(x) = 0.

y(x + a) − f(x)y(x) = 0.

Линейные разностные уравнения второго порядка, yn = y(n)

yn+2 + ayn+1 + byn = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.

yn+2 + ayn+1 + byn = fn. Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + ay(x + 1) + by(x) = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + ay(x + 1) + by(x) = f(x). Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.

y(x + 2) + a(x + 1)y(x + 1) + bx(x + 1)y(x) = 0.

Решение обыкновенных линейных разностных уравнений

с постоянными коэффициентами

Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами

,

где y[ n] - выходной сигнал в момент n ,

x[ n] - входной сигнал в момент n ,

a i , b k – постоянные коэффициенты.

Для решения таких уравнений могут использоваться два метода

• Прямой метод,
• Метод Z – преобразования.

Вначале рассмотрим решение линейного разностного уравнения с помощью прямого метода.

Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения

Общее решение однородного разностного уравнения (zero- input response ) y h [ n]

определяется в виде

.

Подставляя это решение в однородное уравнение, получаем

Такой полином называют характеристическим полиномом системы. Он имеет N корней . Корни могут быть действительными или комплексными и некоторые корни - совпадающими (кратными).

Если корни являются действительными и разными, то решение однородного уравнения имеет вид

где коэффициенты

Если некоторый корень, например, λ 1 имеет кратность m , то соответствующий ему член решения приобретает форму

Если все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням можно представить (записать) в виде , при этом коэффициенты A, B определяются по начальным условиям.

Вид частного решения y p [ n] уравнения зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице

Таблица 1. Вид частного решения для различного характера правой части

Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности и временного сдвига. В результате получается линейное алгебраическое уравнение относительно Z - изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.

Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.

Пример . Определим отклик (выходной сигнал) системы, описываемой линейным разностным уравнением , на входной сигнал

Решение .

1. Прямой метод решения уравнения.

Однородное уравнение . Его характеристический полином .

Корни полинома .

Решение однородного уравнения .

Поскольку,то частное решение определяем в виде .

Подставляем его в уравнение

Для нахождения константы К примем n = 2 . Тогда

Или , К=2,33

Отсюда частное решение и общее решение разностного уравнения (1)

Найдем константы С 1 и С 2 . Для этого положим n = 0 , тогда из исходного разностного уравнения получаем . Для данного уравнения

Поэтому . Из выражения (1)

Следовательно,

.

Из выражения (1) для n = 1 имеем .
Получаем следующие два уравнения для С 1 и С 2

.

Решение этой системы дает следующие значения: С 1 =0,486 и С 2 = -0,816.

Следовательно, общее решение данного уравнения

2. Решение методом Z – преобразования.

Возьмем Z – преобразование от исходного разностного уравнения , учитывая свойство (теорему) временного сдвига 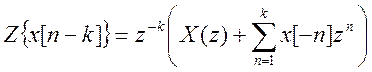. Получаем

Р а з н о с т н ы м у р а в н е н и е м наз. уравнение вида

где - искомая и F - заданная функции. Замена в (2) конечных разностей их выражениями через значения искомой функции согласно (1) приводит к уравнению вида

Если , т. е. уравнение (3) действительно содержит как , так и , то уравне-вие (3) наз. р а з н о с т н ы м у р а в н е н и е м m-го п о р я д к а, или д и ф ф е р е н ц и а л ь н о-р а з н о с т н ы м у р а в н е н и е м.

(6)

где - произвольные постоянные.

3) Общее решение неоднородного Р. у. (4) представляется в виде суммы какого-либо частного его решения и общего решения однородного Р. у. (5).

Частное решение неоднородного уравнения (5) можно построить, исходя из общего решения (6) однородного уравнения, путем применения метода вариации произвольных постоянных (см., напр., ). В случае Р. у. с постоянными коэффициентами

можно непосредственно найти тлинейно независимых частных решений. Для этого рассматривается харак-теристич. уравнение

и ищутся его корни . Если все корни простые, то функции

образуют линейно независимую систему решений уравнения (7). В случае, когда - корень кратности r, линейно независимыми являются решения

Если коэффициенты а 0 , a 1 , . . ., а т действительные и уравнение (8) имеет комплексный корень, напр. простой корень , то вместо комплексных решений выделяют два линейно независимых действительных решения

Пусть имеется Р. у. 2-го порядка с постоянными действительными коэффициентами

(9) Характеристич. уравнение

имеет корни

Общее решение уравнения (9) в случае удобно записывать в виде

(10)

где с 1 и с 2 - произвольные постоянные. Если и - комплексно сопряженные корни:

то другое представление общего решения имеет вид

В случае кратного корня общее решение может быть получено предельным переходом из (10) или (11). Оно имеет вид

Как и в случае уравнений произвольного порядка, для Р. у. 2-го порядка можно рассматривать задачу Коши или различные краевые задачи. Напр., для задачи Коши